My current research activities involve the following fields in condensed matter physics and statistical physics:
(1) Exotic states of matter in two-dimensional (2D) frustrated magnetic systems such as quantum spin liquids and novel magnetic ordered states;
(2) Fractional quantum Hall effects and fractional statistics;
(3) Numerical characterizations of topological ordered states using state-of-the-art methods;
(4) Quantum criticality, quantum fluctuations, quantum phase transitions and conformal invariance;
(5) Applications of quantum information concepts to quantum many-body systems, understanding the emergent phenomena via the lens of quantum entanglement;
(6) Non-equilbrium phenomena in quantum many-body systems, quantum dynamics.
Below is a short synopsis of my recent work towards reaching the aforementioned research goals.Exotic states of matter in 2D frustrated magnetic systems
Quantum spin liquid is an exotic state of matter that escapes from forming normal magnetic order in frustrated magnetism. In the study of spin liquid, it is highly challenge to uncover its topological nature in a spin-disordered ground state.
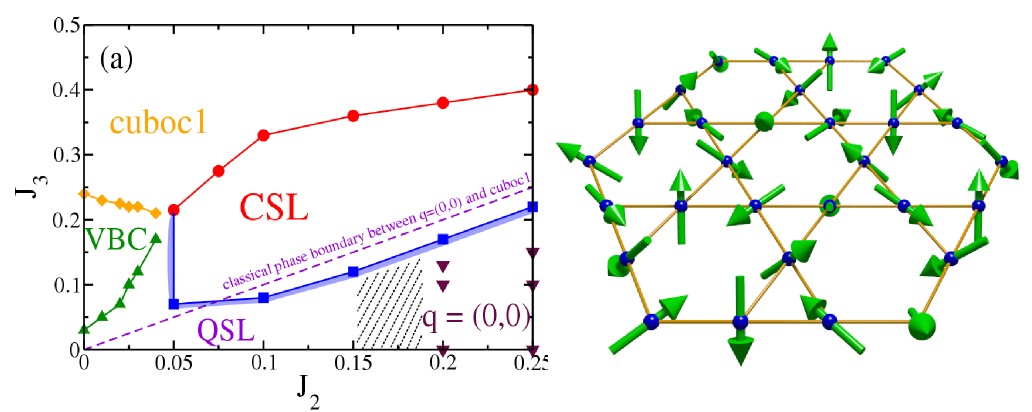
We systematically studied a series of 2D frustrated magnetic systems using the unbiased numerical calculations. In a spin-1/2 kagome Heisenberg model with extended couplings, we discovered a chiral spin liquid (CSL) that is topologically equivalent to the v=1/2 bosonic Laughlin state, which is the first example of gapped spin liquid in realistic Heisenberg model and may be realized in the magnetic materials [Sci. Rep. 4, 6317 (2014)]. By studying the global quantum phase diagram of this model, we found that the CSL emerges between an usual coplanar magnetic ordered state and an unusual non-coplanar magnetic ordered cuboc1 state that also breaks time-reversal symmetry [Phys. Rev. B 91, 075112 (2015)]. To understand this CSL in theory, we constructed the parton wavefunction for this CSL and performed a variational calculation to confirm its topology [Phys. Rev. B 91, 041124(R) (2015)]. Furthermore, we constructed various different models, e.g. a kagome model with the extended XY interactions [Phys. Rev. B 92, 014424 (2015)], a triangular model with spin chiralities [ Phys. Rev. B 96, 075116 (2017) ], and identified similar time-reversal breaking CSLs there. These results, identifying a novel example of spin liquid, represent a significant progress towards understanding the quantum spin liquids.
Besides the chiral spin liquid, we also put exhausted efforts on the gapless Dirac spin liquid in frustrated Heisenberg models. For example, by advancing numerical techniques, we successfully identified both of Dirac spinon and monopole excitations of a U(1) Dirac spin liquid on triangular Heisenberg model [Phys. Rev. Lett. 123, 207203 (2019) ]. This is a non-trivial achievement that has never been reached before. Moreover, in the square Heisenberg model, the intermediate non-magnetic phases was identified as the plaquette-valence-bond state, which breaks lattice translational symmetry. [ Phys. Rev. Lett. 113, 027201 (2014)].
Non-Abelian states in Fractional Quantum Hall Effect
The non-Abelian topological order has attracted a lot of attention for its fundamental importance and exciting prospect of topological quantum computation. Despite the great potential applications, many of the basic and practical questions remain open. They must be resolved in order for these ideas to become a reality, and they touch upon fundamental issues in physics. The first question is whether the non-Abelian topological phases actually exist in nature and specifically, in quantum hall systems.
One promising candidate for finding non-Abelian statistics seems to be the fractional quantum Hall state observed at the ν=12/5 plateau. In a recent paper [ Phys. Rev. Lett. 115, 126805 (2015)], we presented what we believe to be compelling evidence that the essence of the Coulomb-interaction ground states at ν = 13/5 and 12/5 is indeed captured by the parafermion k = 3 Read-Rezayi state, in which quasiparticles obey non-Abelian “Fibonacci-anyon” statistics.
Interface between two states of matter is an amazing playground that could give birth to exotic phenomenon. Motivated by this idea, we propose to investigate the interface between two topologically distinct non-Abelian quantum Hall states. We demonstrate an intrinsic electric dipole moment emerges at the interface, similar to the “p-n” junction sandwiched between N-type and P-type semiconductor. Importantly, we elucidate the topological origin of this dipole moment, whose formation is to counterbalance the mismatch of guiding-center Hall viscosity of bulk Pfaffian and anti-Pfaffian state [Phys. Rev. Lett. 125, 146802 (2020) ].
Another quasi-realistic microscopic model hosting non-Abelian topological orders is the topological flat-band lattice model or fractional Chern insulator. We provided a complete characterization of the universal properties of bosonic Moore-Read state in Haldane honeycomb lattice model, including both the edge spectrum and the bulk anyonic quasiparticle statistics (such as braiding statistics, topological spin) [ Phys. Rev. B 92 165106 (2015)]. We also investigate the possibility of realizing non-Abelian states in double-layer systems by coupling two Abelian fractional quantum Hall states together. We find partial evidences of non-Abelian Moore-Read state by tuning the tunneling strength between two layers, for example [ Phys. Rev. B 91, 245126 (2015) and Phys. Rev. B 94, 245147 (2016) ].
The lens of Quantum Entanglement
Very recently, more and more evidences support that the quantum entanglement is intrinsic to quantum states with emergent macroscopic properties, such as the existence of excitations with fractional electric charge and statistics. This inspires growing interests on characterizing correlated systems through the quantum entanglement information.
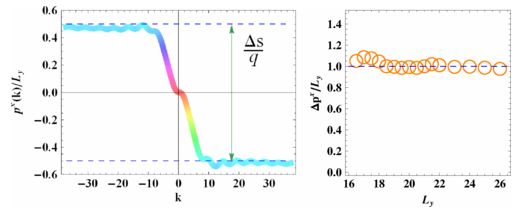
We explored and developed a scheme to extract the anyonic statistics of underlying topological order on lattice systems. We numerically validated the one-to-one correspondence between minimal entangled states and quasiparticle eigenstates in various Abelian systems [ Phys. Rev. B 88, 035122(2013)] and non-Abelian systems [ Phys. Rev. Lett. 112, 096803 (2014)]. This method provides a unbiased way to get the full information of a given topological order, which is crucial to characterize the underlying anyonic statistics in lattice models.
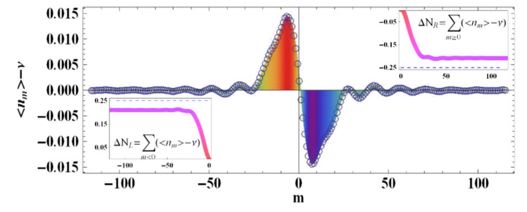
We attempted a numerical Aharonov-Bohm experiment on quantum spin models, and uncovered universal entanglement signatures of emergent Dirac spinons, which are the fractionalized excitations of the quantum spin liquid. This scheme provides qualitative insights into the nature of kagome quantum spin liquid and can be used to study other quantum states of matter. [ Sci. Adv. 2018;4: eaat5535 ]
Quantum Criticality
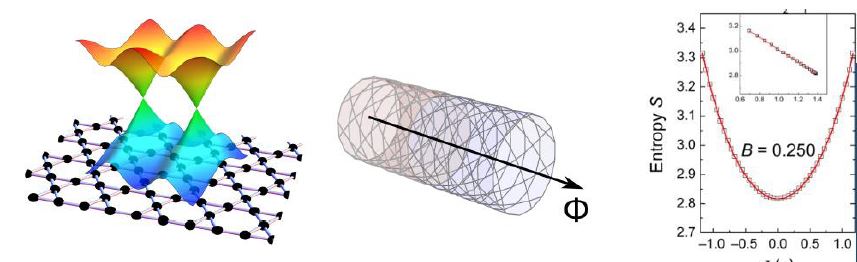
Phase transitions and related critical phenomena originate from collective behavior of interacting particles, the study of which is generally challenging in statistical and condensed matter physics. Interestingly, if a novel conformal symmetry—a symmetry that can change shapes while maintaining angles—emerges at the phase transition point, numerous insights into critical behaviors can be inferred by using conformal field theory (CFT). This approach has been very successful in 2D systems, however, the emergence and appearance of conformal symmetry in higher dimensions is rarely studied, mainly due to unavoidable mathematical or conceptual obstructions.
Recently, we propose and design an innovative theoretical scheme to study the 3D phase transition on a spherical geometry, wherein the physics of conformal symmetry becomes transparent [Phys. Rev. X 13, 021009 (2023)]. Our findings reveal the telltale signs of emergent conformal symmetry at the phase transition point, and, notably, we achieve a rich understanding of the 3D Ising phase transition at an astonishingly low computational cost.
Quantum Dynamics
Quantum dynamics out-of-the-equilibrium is a fast-evolving field, where many open problems are fundamental to statistical mechanism. A powerful perspective in understanding nonequilibrium quantum dynamics is through the time evolution of its entanglement content, examples ranging from entanglement entropy to entanglement spectrum. One active direction is to develop new entanglement-based methods to study quantum dynamics.
We explore signatures of the entanglement evolving and information propagating out of equilibrium, from the view of the entanglement Hamiltonian [Phys. Rev. Lett. 124, 100605 (2020)]. This new advance has not been studied before, which encodes many unique characters. For example, the emergent current operator and entanglement temperature reflect entanglement spreading process towards equilibrium. These findings not only provide crucial information on how equilibrium statistical mechanics emerges in many-body dynamics, but also add a tool to exploring quantum dynamics from the perspective of the entanglement Hamiltonian.
Based on the conformal field theory, we discover some universal signatures of entanglement spectra in the quantum quench dynamics. In particular, the time evolution of entanglement spectra allows to extract conformal information of underlying quantum critical point [Chinese Physics Letter 37, 100037 (2020) [Express Letter] ]. Our findings, for the first time, provides an intuition that conformal information can be extracted from quantum dynamics. To our best knowledge, the above achievement is really rare.

Novel Phases Driven By Electron-Electron Interactions
Non-interacting topological states of matter can be realized in band insulators with intrinsic spin-orbital couplings or external magnetic field as a result of the nontrivial band topology. In recent years, the possibility of realizing novel interaction-driven topological phase has attracted a lot of research activities, which can significantly enrich the classes of topological materials and is thus of great importance.
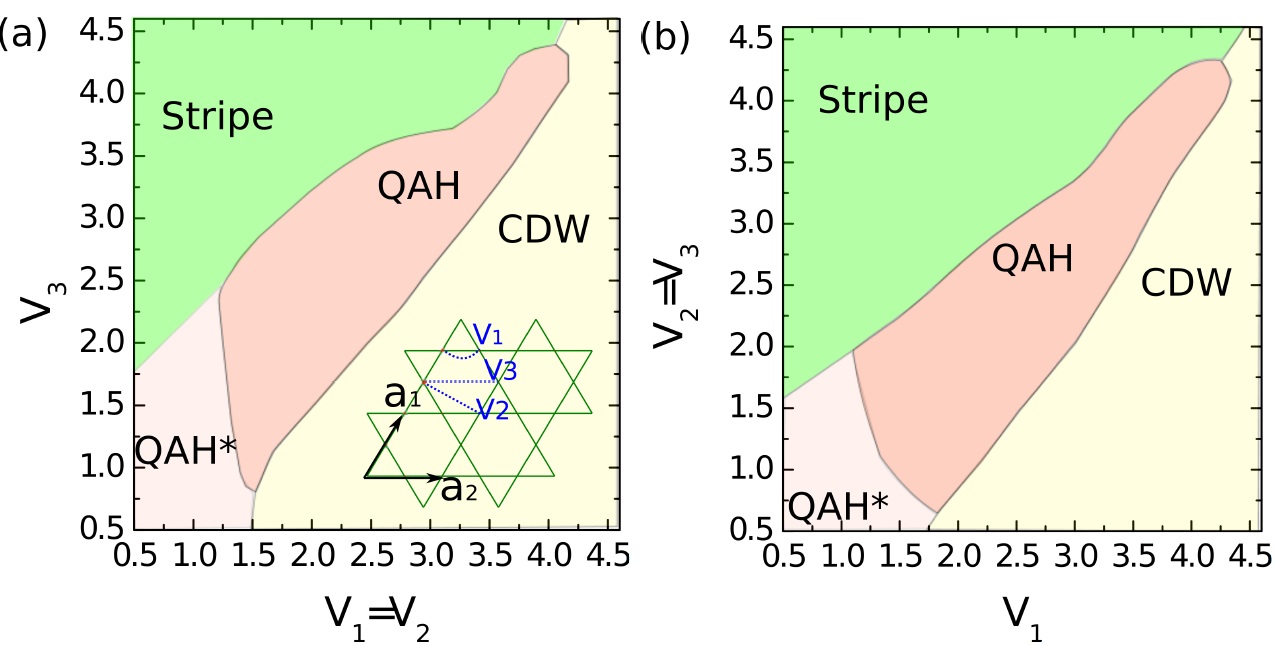
In our recent work [Phys. Rev. Lett. 117, 096402 (2016)], we propose an extended fermionic Hubbard model on kagome lattice, and unveil the nature of ground state is equivalent to the quantum anomalous Hall state. This serves as the first solid evidence of topological Mott insulator from a microscopic view of point. Significantly, this work provides a “proof-of-the-principle” demonstration of interaction-driven topological phase in a “gauge-field-free” non-interacting band, without the requirement of external magnetic field or other mechanism of time-reversal symmetry explicit breaking.